李 飞，林 成

辽宁石油化工大学机械工程学院,抚顺 113001

摘要

自从1978年吉林大学的余瑞璜院士建立“固体与分子经验电子理论”(简称余氏理论)以来，余氏理论已被广泛应用于材料科学研究中。余氏理论作为目前唯一由我国学者建立的比较完善的电子理论，它的快速健康发展对提升我国材料电子理论在国际上的地位与水平具有重要的意义。

余氏理论的基本思想来源于量子力学、能带理论、电子浓度理论及价键理论。该理论建立了固体与分子中原子状态的描述方法，给出了固体与分子中原子状态的表征方法，建立了多粒子体系的原子间相互作用方程与求解方法。然而，余氏理论的一些“经验因素”制约着其发展与进步。经过40余年的发展，这些“经验因素”已经越来越少，但研究者们还未关注到余氏理论的持续研究进展。

目前，余氏理论已不断地完善与发展，其中自洽键距差法和界面电子结构的计算极大地丰富了余氏理论的内涵。余氏理论的研究范围也比较广泛，几乎包含了所有合金体系。基于余氏理论的合金成分设计方法研究，使余氏理论的研究更具有实用性。迄今为止，余氏理论的发展正经历三个阶段，即理论初始的建立期、20世纪90年代的理论广泛应用期以及当今的理论发展缓慢期。

为了进一步推动余氏理论的发展与进步，本文从余氏理论的理论基础出发，详细地论述了余氏理论的主要内容与思想精髓，深入分析了余氏理论的不足与解决思路，归纳总结了余氏理论的最新研究成果，展望了余氏理论的发展趋势。本文的研究报道不仅为余氏理论的研究者提供可借鉴的研究思路，也有利于余氏理论的不断进步与发展。

引言

基于量子力学、能带理论、电子浓度理论及价键理论，吉林大学余瑞璜院士对上千种物质的性质、热力学参数进行归纳总结，并于1978年建立了“固体与分子经验电子理论”(简称EET或者余氏理论)。目前，该理论已经广泛应用到材料的固溶体、化合物、超硬材料、相变、相图、组织形态及分布、凝固、合金界面、耐蚀性、表面改性、焊接性、强韧化机制及力学性能等研究。同时对材料的熔点、导电、光学、磁学、表面、结合能等物理性能也进行了大量的研究。然而，在当前材料科学迅猛发展的态势下，余氏理论的发展仍处于停滞不前的状态。众多研究者对余氏理论困惑的主要原因有如下几点：①对余氏理论基础认识不清；②对余氏理论中的“经验因素”因认识不足而夸大其词；③对余氏理论的价电子结构因理解不透彻而运用不充分。基于上述问题，本文重点介绍了余氏理论的理论基础、余氏理论中“经验因素”及其解决策略、余氏理论的未来发展趋势等，为推动余氏理论的快速发展提供可借鉴的思路。

1.余氏理论的理论基础

余氏理论打破了化学和物理学科的界限，将价键理论、量子力学及固体物理学等进行了衔接与互补，实现了从自由原子状态到实际固体中原子状态及原子间相互作用的表征、推演及求解。图1给出了余氏理论体系的结构图。从图1可以看出，余氏理论从自由原子状态的描述出发，给出了固体中原子(受约束原子)的描述方法，改进了描述原子间相互作用势的键距方程，建立了描述多体系原子间相互作用的原子精细价电子结构及体系能量，从而利用精细价电子结构及体系能量实现对体系宏观性质的描述与表征。

 

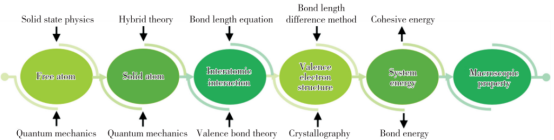
图1 余氏理论体系结构图

1.1自由原子的描述

余氏理论中自由原子的描述与原子物理学的描述方法相一致，主要涉及量子力学、泡利不相容原理、能量最低原理和洪特规则等基本原理及其结论。元素周期表中各种原子的基态所对应的未满层中的电子组态是余氏理论描述原子状态的基础，余氏理论原子状态杂化时的两个杂化双态均来源于自由原子的基态和激发态。

1.2固体中原子的描述

当自由原子受到其他原子约束时，原子间的相互作用将使自由原子变成受约束原子(亦称固体中的原子)，同时也能引起原子内电子状态发生复杂变化。但是固体中的原子也需要遵循泡利不相容原理和能量最低原理，这就会使固体中原子内部的闭壳层(被电子完全填满的壳层)上的电子排布基本保持与自由原子状态时的相一致；而固体中原子性质的复杂变化主要来源于外部未满壳层上电子排布的改变，分布在未满壳层的电子被称为价电子。于是，余氏理论将闭壳层电子与原子核作为芯(或离子实)，并与外壳层的价电子分开处理。这种简化处理为余氏理论求解复杂体系原子间相互作用提供了捷径。

余氏理论根据价电子在实际中的作用和特点，将价电子分为哑对电子、磁电子、共价电子和晶格电子四类。哑对电子是指价电子层中满轨道且不参与公有化的一类电子(记为n_d)；磁电子是指价电子层中半满轨道的电子(记为n_m)，是磁矩的主要来源；共价电子是价电子层中单占据轨道且参与公有化后能与邻近原子形成公共电子对的一类电子(记为n_c)；晶格电子是指游荡于几个原子组成体系内的价电子(记为n_l)。尽管晶格电子是余氏理论中新引入的概念，但是晶格电子的引入是具有实验基础(NiAl合金、金属Be)和理论证实的。在这四类价电子中，哑对电子、磁电子是保持在原来原子内的原子式电子；而共价电子、晶格电子是离域电子，参与公有化，只不过晶格电子并不分布在“键”上。

当自由原子变成受约束的原子后，原子的价态变化可以由上述四类价电子进行表征。在原子价态发生变化的同时，受约束的原子的尺寸也将发生变化，这种尺寸改变的描述并不能通过假定原子是一种刚性小球来实现，而往往通过原子最外部的电子密度峰离核距离的变化来反映。于是，余氏理论基于原子的共价半径和金属半径数据，引用元素的共价半径(亦称单键半距)来表征受约束原子的原子尺度特征。余氏理论给出了元素的单键半径值，当然这里包含了余瑞璜院士的一些经验认识与积累。

余氏理论中的等效价电子概念与原子物理学中的等效电子概念是截然不同的。原子物理学中往往将具有相同主量子数(n)和角量子数(l)的电子称为等效电子；而余氏理论中的等效价电子是指根据价电子的空间轨道分布特征而产生的功能等效。该理论中，主要有两种等效价电子。一种是等效于s或p的d电子，该种等效的原因是某些原子的外层d轨道电子发生畸变与扩展，对共价键距的影响等同于外层的s或p轨道电子。另一种是等效于s的p电子，这种等效的原因是有些元素的p轨道电子比较混乱，统计平均效应与s轨道电子相当。常用元素的等效价电子假定已在余氏理论杂化表中给出。

至此，余氏理论利用四类共价电子、单键半距及等效价电子假设实现了从原子的价态特征和尺寸特征来描述固体与分子中的原子(受约束的原子)。当原子处于某个定态时，该原子应该具有确定的原子特征参量，如共价电子数n_c、晶格电子数n₁、磁电子数n_m、哑对电子数n_d及单键半径R(1)。那么，对于每种元素在自然界中到底存在多少种原子状态?每种状态下原子的特征参量如何表征?余氏理论借助泡利的杂化理论给出了上述两个问题的答案。

1.3余氏理论的原子杂化

在余氏理论中，受约束原子的双态杂化与泡利自由原子的双态杂化相似，不同之处为余氏理论选取的杂化双态h态和t态是已被简并态s，p，d，…的久期扰动杂化过的。与自由原子状态一样，固体和分子中的原子也具有一系列不同的定态。于是，余氏理论在h态和t态基础上进一步久期扰动产生了新的原子杂化态，这种进一步久期扰动便是固体与分子中原子状态的不连续假定(即K公式)。

杂化概念在原子物理学及固体物理中经常使用，但是这些学科中的杂化与余氏理论中的杂化既有联系又有差别。前者主要涉及各价层中原子轨道s，p，d，…间的杂化，参与杂化的各原子轨道的成分是任意变化的，这些成分系数可以通过量子力学的久期方程确定。而余氏理论的杂化是不同原子状态间的杂化，参与杂化的原子状态中各轨道的成分是固定的，但是参与杂化的两个态的成分是变化的，求解参与杂化态成分无需求解久期方程。实际上余氏理论中参与杂化态的成分一旦确定，原子轨道杂化也便确定，因此余氏理论的双态杂化也是一种原子轨道杂化。

在泡利杂化理论基础上，余瑞璜院士从量子力学角度推导出余氏的原子状态不连续假定(即K公式)。该假定认为，原子的双态杂化可以改变原子轨道的成分，使电子云沿着两原子成键的方向达到键的加强；而特定晶体结构中要保持原子成键轨道稳定，参与杂化双态的成分应该是不连续的。利用K公式可以实现固体与分子中原子状态的精细描述：①确定出的某种原子在特定情形下具有稳定杂化状态(台阶或者杂阶)的数目；②求解出在每个稳定杂化状态(杂阶)下参与杂化h态和t态的成分；③给出在每个稳定杂化状态下原子特征参量(n_Tδ，n_lδ，n_cδ，R(l)_δ)，实现约束原子的精细描述。

余瑞璜院士根据上千种晶体与分子的结构、晶体的力学性能和物理性能、泡利化学键理论、能带理论等研究结果，归纳总结给出了元素周期表中常用元素的杂化双态，并利用K公式给出了上述元素的原子特征参量，并汇总成杂化表，该表是余氏理论计算的基础资料。

1.4多粒子体系的原子间相互作用

分子和固体是由强烈相互作用的原子组成的多粒子体系，这种原子之间的强烈相互作用称为化学键。通常，化学键分为共价键、离子键和金属键。在实际多粒子体系中，大多数情况下原子间相互作用是这三种共价键的混合。余氏理论在处理这三种化学键时认为离子键、金属键是共价键的特殊情况，本质与共价键一致，并给出了相应的实验证据。

余瑞璜院士基于泡利等在键距方面的工作，给出了余氏理论的两原子间键距公式，即：

 

通过式(1)可以给出体现多体系原子间相互作用的方程组，但是针对如何求解这些方程组及如何确定各原子在多粒子体系约束下的杂化状态，余瑞璜提出了求解固体与分子中精细价电子结构的分析方法，即键距差(BLD)法。BLD法的基本思想包括三点：①为了维持体系结构的稳定性，在同一体系中各共价键上的共用电子数的分配规律应该是相对固定的，即各共价键上共用电子对数相对比值是相对固定的；②体系内应满足电子守恒规律，即在体系内原子所贡献的全部共价电子应该完全分配到各条共价键上；③体系应该满足余氏判别式∆D≤0.005nm的条件，即理论键距与实验键距之差(∆D)应该符合余氏判别式。但该判别式的最大问题是其使余氏理论产生了多重解。对于余氏的多重解，程开甲院士曾从量子力学变分方法推导出余氏判别式也是能量E极值的泛函分析结果，并不是随意拼凑的，而是第一性原理的必然结果。但是多重解仍对研究者在实际中运用余氏理论带来太多的麻烦。

余氏理论利用BLD法给出了分子和固体体系内各组成原子所处的原子状态、实空间中共价电子及晶格电子分布等，这些统称为价电子结构。利用价电子结构，余氏理论给出了共价键能及晶体的结合能计算方法，从而实现了固体体系中各种行为的定性及定量研究。

 

2.余氏理论中“经验因素”及其完善

余瑞璜院士之所以将余氏理论命名为“固体与分子经验电子理论”，考虑的几个方面如下：

(1) 原子双态杂化的构建；

(2) 元素的单键半径R(l)计算公式及键距方程中的参数β值；

(3) 从多重解中确定体系最可能的原子状态。

在上述三方面，余氏理论中确实存在着“经验因素”，并且这些“经验因素”也一直制约着该理论的发展。其实，经过40余年的发展，余氏理论中的“经验因素”已经越来越少，只是目前广大研究者还未充分意识和关注到余氏理论的持续研究进展。

针对上述三点经验因素，笔者结合研究经历谈谈自己的三点体会：

(1) 如前所述，余氏理论的杂化双态(h态和t态)来源于自由原子的杂化态。但是从自由原子的一系列定态中，如何选取h态和t态是余先生根据实验结果及自己经验确定的。考虑到余氏杂化与泡利杂化的差别，余瑞璜教授在泡利公式基础上提出了余氏改进的单键半径R(l)计算公式，其中z’和z”的取值是余先生根据经验确定的。在考虑了原子双态杂化和元素单键半径的经验后，余瑞璜院士建立了周期表中大部分元素的原子状态杂化表，这是余氏理论研究的基础。从目前来看，余氏理论的广泛应用也验证了上述经验因素的提出是值得信赖的。

(2) 尽管程开甲院士已经证明了余氏判别式是第一性原理的必然结果，但因余氏判别式给出的多重解一直饱受学术界的诟病，诚然在众多满足余氏判别式条件下的原子组态中挑选出一组合适的解也的确十分困难与随意。于是，Lin等将“等概率原理”引入到余氏的BLD法中，解决了余氏理论的多重解问题。

(3) 余氏键距方程中的β是一个很重要的参数，它与余氏理论中多体势函数的合理与否有关。尽管余先生对β参数的确定给出了明确的规则，但是很多研究者仍担心其合理性，于是Lin等将“迭代自洽场”、“等概率原理”同时引入到余氏的BLD法中，提出自洽键距差法(SCBLD)。该种方法的优点之一就是通过计算机软件可以获得优化的β参数，而不由人为经验规定。

3.余氏理论的发展现状

3.1余氏理论体系的丰富

余氏理论发展至今已40余年，研究者已经意识到它的不足，并进行了诸多改进、完善与丰富工作，其中比较典型的几个方面如下：①余氏理论本身的完善与发展；②界面电子结构的计算，将余氏理论由晶内研究推广到界面研究；③在钢铁、钛合金领域提出基于余氏理论的合金成分设计方法，这将余氏理论研究推向更复杂、更切合实用的研究水平；④研究范围比较广泛，已经几乎包含了所有合金体系。当然有些完善工作还处于起步阶段，但也确实为余氏理论注入了新的思想，必将推动余氏理论更为广泛地应用。

3.2余氏理论的研究队伍与研究成果

迄今为止，余氏理论的发展正经历三个阶段，即理论初始建立期、20世纪90年代理论广泛应用期以及当今的理论发展缓慢期。在余氏理论建设初期，理论创立者余瑞璜院士带领张瑞林、郑伟涛等利用余氏理论研究了材料的相图、熔点、结合能、导电性、磁性等，开辟了余氏理论的先河，吸引了众多学者对余氏理论的兴趣。

在1990年以后，以刘志林教授、李志林教授为代表的广大研究者将余氏理论广泛应用到材料科学研究中。他们先后提出了合金相及相界面的电子结构计算模型，开展了余氏理论在材料科学领域中的广泛应用研究，并提出了合金力学性能理论计算与成分定量设计的思路。截至2010年左右，国内大概有十几所高等院校和研究所开展过余氏理论的研究工作。然而，最近几年从事余氏理论研究的团队越来越少，这也是余氏理论发展缓慢的主要原因之一。

 

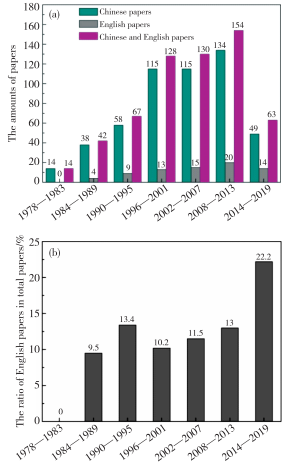
图2  余氏理论发表文章数:

( a) 中、英文章数目；( b) 英文文章数占文章总数的比例

图2为从事余氏理论的研究者在1978—2019年间国内、国际期刊发表相关论文的情况。总体看，有关余氏理论的被发表的研究论文还比较少，共计在600篇左右(图2a)；在1996—2013年期间，有关余氏理论方面的论文数达到最大值，每五年在120~150篇左右，而最近几年又呈现明显下降趋势。这可能是因为在1996—2013年间，从事余氏理论研究的科技工作者较多，获得经费资助也相对较多，而在近几年中从事余氏理论的研究者获得经费资助的机会比较少，因此从事该方面研究的热情和人员显著下降，相关方面的科技论文发表也比较少。另外，从图2b可以看出，余氏理论方面发表的英文论文篇数占发表论文总数仍不足25%，这也是余氏理论发展缓慢的主要原因之一；但是余氏理论从建立到如今，其英文论文的数量还是逐渐提高的，尤其是在2014年以后余氏理论方面的英文论文数量增加近2倍，这也表明余氏理论的影响力还是逐渐提升的。

4.结语与展望

综上所述，余氏理论也可以被认为是第一性原理的一种近似方法。余氏理论在处理复杂的合金体系时具有其独特的优势：(1)不必构建复杂的势函数；(2)给出体系中电子实空间分布情况，更适合各向异性材料研究；(3)适合讨论材料相变时原子的运动趋势及路径。

当然，余氏理论的发展也面临一些困难。如：余氏理论的认知度较低，研究者比较少；余氏理论对未知晶体结构的研究仍比较少；余氏理论给出的电子结构参数表征物质宏观性质的理论体系仍不完备，尤其是磁、光、电等。

余氏理论发展至今已达40年之久，尽管发展过程中出现了诸多困难，但迄今它仍然活跃在计算材料的舞台上，说明余氏理论还是具有生命力的，它的优势还是深受研究者认可的。在广大研究者的参与推动下，余氏理论中的经验因素会越来越少，理论的应用层次和领域也会越来越上一个台阶。从事余氏理论的研究者应博采众长、吐故纳新，为余氏理论的发展不断注入新鲜血液。相信余氏理论未来一定能在百花齐放、百花争鸣的计算材料学舞台上发挥其重要作用。

原文载于：材料导报 2020,Vol. 34,No. 7 

 

编校 | 周 淼

排版 | 于 跃

审核 | 侯博宇、杨 景